Bias/Variance Tradeoff is a concept in machine learning which refers to the problem of minimizing two major sources of errors at the same time and prevent the supervised learning algorithms from generalizing to accommodate inputs beyond the original training set.

The two error sources here are:

• Bias
• Variance

Sources of Error

Bias Error (Underfitting):

In case of underfitting, the bias is an error from a faulty assumption in the learning algorithm. This is such that when the bias is too large, the algorithm won’t be able to correctly model the relationship between the features and the target outputs.

Variance Error (Overfitting):

In case of overfitting, the variance is an error resulting from fluctuations in the training dataset. A high value for the variance would cause the algorithm may capture the most data points put would be generalized enough to capture new data points.

How do we adjust these two errors so that we don’t get into overfitting and underfitting?

One way to reduce the error is to reduce the bias and the variance terms. However, we cannot reduce both terms simultaneously, since reducing one term leads to increase in the other term. This is the idea of bias/variance tradeoff.

Relationship to underfitting and overfitting

If the model is too complex, then it will pick up specific random features (noise or example) in the training set. This is overfitting.

If the model is not complex enough, then it might miss out on important dynamics of the data given. This is underfitting.

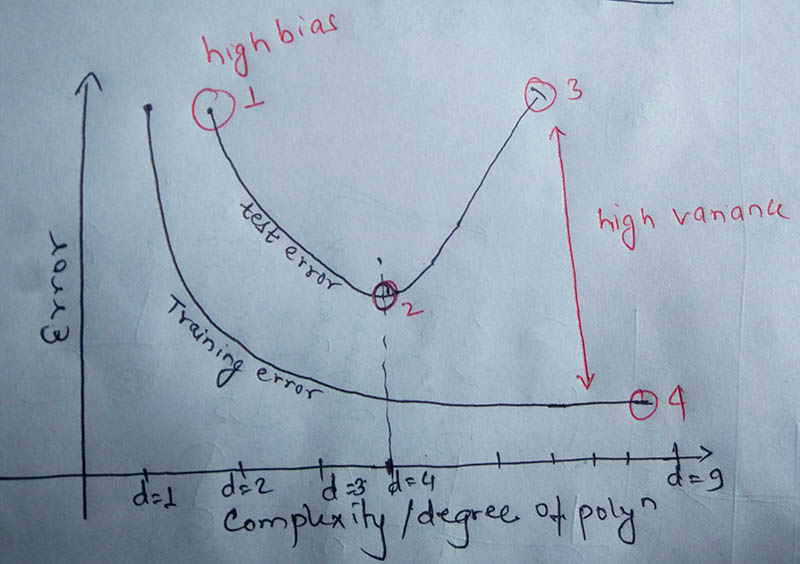
Bias-Variance tradeoff Graph Explained

In the above image:
1. indicates high bias
2. indicates optimal model complexity
3. high test error
4. very low training error

How to solve High bias and high variance problem?

In order to solve high bias, we have to change the entire model. While high variance could be solved by increasing the training data set. The larger the training data set less is the testing error.

Advice for machine learning from Andrew Ng:

If you run a learning algorithm and it does not do as well as you are hoping, almost all the time it will be because you have either a high bias problem or a high variance problem. In other words, they’re either an underfitting problem or overfitting problem.

Please follow the below links to know in detail:

Video 1:

Video 2:

Video 3: